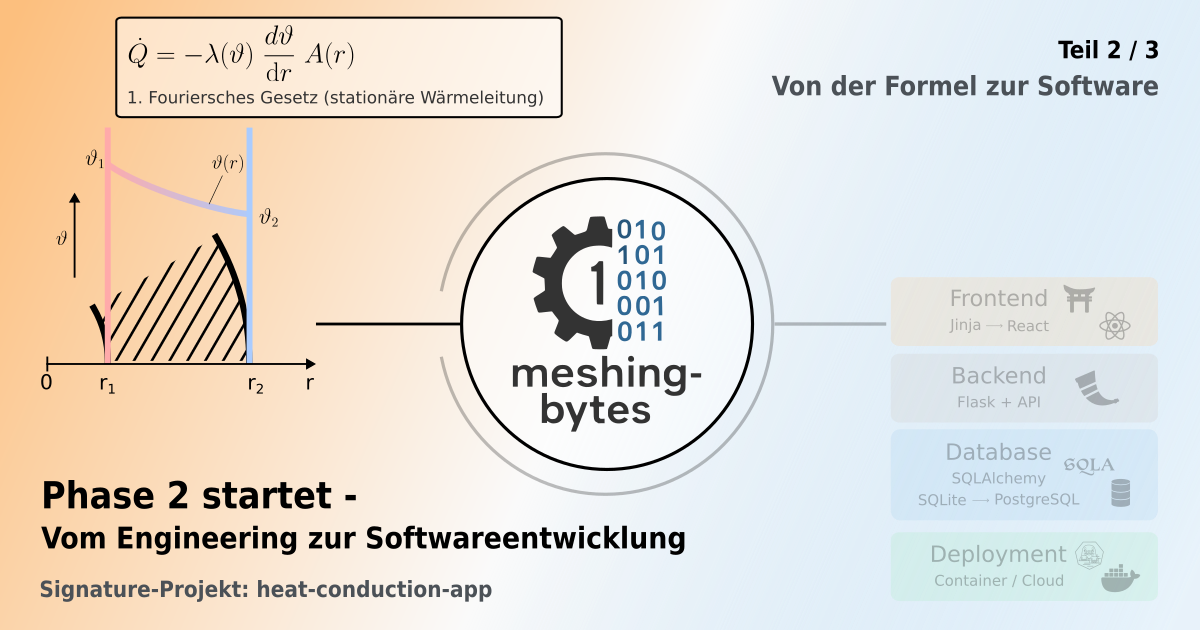
Teil 2 / 3
Wie sich das Fouriersche Gesetz in Software übersetzen lässt
Phase 2 startet - Vom Engineering zur Softwareentwicklung - Projekt heat-conduction-app
Wärmeübertragung Berechnung Engineering → Softwareentwicklung heat-conduction-app
Einleitung
Im ersten Teil meines Einführungsposts ging es mir um meinen persönlichen Entwicklungsweg vom Diplom-Maschinenbauingenieur zum selbstständigen Softwareentwickler mit dem Ziel, Ingenieurwissen und moderne Softwareentwicklung zusammenzuführen. Ein zentrales Element dieser neuen beruflichen Phase ist die heat-conduction-App, die als Demo-Anwendung und Architektur-Referenzprojekt dient.
In diesem zweiten Teil möchte ich auf den technischen Kern eingehen, den physikalischen Hintergrund der App und den Weg von der technischen Formel hin zur Softwarearchitektur. Das Thema Wärmeleitung, oder allgemeiner Wärmetransport, ist physikalisch sehr umfangreich und verdient sicher einen eigenen Artikel, daher beschränke ich mich hier auf die Einführung der vereinfachten stationären, eindimensionalen Form der Wärmeleitung.
Physikalisch-technischer Hintergrund - das 1. Fouriersche Gesetz
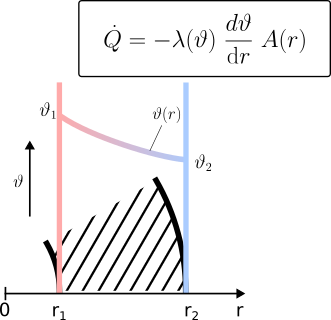
Das physikalische Grundprinzip, das der Demo-App zugrunde liegt: die stationäre, eindimensionale Wärmeleitung durch eine homogene Wand, begegnet uns alltäglich und insbesondere bei technischen Geräten.
Zwischen den beiden Wandseiten mit den Temperaturen \(\vartheta_1\) und \(\vartheta_2\) fließt Wärme von der warmen zur kälteren Seite. Diese Form des Wärmetransports wird Konduktion oder Wärmeleitung genannt. Sie entsteht durch Energieübertragung auf atomarer Ebene, ohne dass sich das Material selbst bewegt, im Gegensatz zur Konvektion (wärmeübertragender Stoffstrom) oder Strahlung (elektromagentische Übertragung).
Die Grundlage bildet das 1. Fouriersche Gesetz in seiner eindimensionalen, stationären Form:
\[ \dot{Q} = \lambda(\vartheta) \cdot \frac{ \mathrm{d}\vartheta}{\mathrm{d}r} \cdot A(r) \]
mit den Vereinfachungen:
- Eindimensionale Wärmeleitung (1D) - Es findet nur Wärmetransport in einer Richtung statt
- Stationärer Zustand - Temperaturen und Wärmeströme ändern sich zeitlich nicht
Dabei beschreibt:
- \(\dot{Q}\) die übertragene Wärmestromleistung
- \(\lambda(\vartheta)\) die temperaturabhängige Wärmeleitfähigkeit des Materials
- \(\frac{ \mathrm{d}\vartheta}{\mathrm{d}r}\) den Temperaturgradienten
- \(A(r)\) die Querschnittsfläche entlang des Wegs \(r\)
Um das Prinzip möglichst einfach und nachvollziehbar in einer Software abzubilden, werden in der Demo-App zwei weitere Vereinfachungen vorgenommen:
- Konstante Wärmeleitfähigkeit - \(\lambda\) ist keine Funktion der Temperatur
- Konstante Fläche - ein über den Weg \(r\) konstanter Durchmesser \(A\)
Unter diesen 4 Annahmen vereinfacht sich das Fourier-Gesetz zu einer linearen Gleichung.
\[ \dot{Q} = \frac{\lambda \cdot A \cdot (T_1 - T_2)}{d} \]
Diese Gleichung beschreibt die Wärmeleitung durch eine Wand mit der Dicke \(d\) zwischen den Temperaturen \(T_1\) und \(T_2\).
Warum “nur” die Wärmeleitung durch eine Wand betrachtet wird
Ein Ingenieur könnte nun sagen: “Nur die Wärmeleitung in ihrer einfachsten Form umzusetzen, damit komme ich doch nicht weit.” Und er hätte völlig recht. Die meisten thermischen Berechnungen sind deutlich komplexer. Erweiterungen wie Konvektion, Strahlung, mehrschichtige Systeme, transiente Berechnungen oder ganze thermische Modelle liegen natürlich nahe.
Aber an dieser Stelle geht es mir um etwas anderes. Der Fokus dieser Demo-Anwendung liegt nicht auf der vollständigen physikalischen Tiefe, sondern auf ihrer Architektur als Referenzprojekt. Ich möchte zeigen, wie sich Berechnungen grundsätzlich in eine moderne, modulare Software-Applikation integrieren lassen.
Die 1D-stationäre Wärmeleitung ist dafür ein idealer Startpunkt: Sie ist mathematisch einfach, technisch anschaulich, und trotzdem universell genug, um später erweitert zu werden. Genau das macht sie zu einem hervorragenden MVP (Minimum Viable Product), einer Basisgleichung, die sich leicht skalieren, erweitern und visualisieren lässt.
Aus meiner Erfahrung entwickeln sich solche Tools ohnehin iterativ: Sobald eine funktionierende Grundanwendung existiert, wächst der Wunsch nach zusätzlichen Funktionen. Mit der Zeit kann daraus ein umfangreiches System entstehen und irgendwann steht man vor der Frage, ob man die Aufgaben trennt, Teile auslagert oder über APIs mehrere spezialisierte Apps verbindet.
Die Wärmeleistung durch eine Wand ist also weniger eine inhaltliche Begrenzung, sondern vielmehr ein bewusst gewähltes Fundament, auf dem sich eine nachhaltige Software-Architektur aufbauen lässt.
Von der Formel zur Softwarelogik
Nachdem die technisch-physikalische Aufgabenstellung klar ist, stellt sich die Frage: Wie wird daraus Softwarelogik? An dieser Stelle geht es noch nicht um den konkreten Technologiestack, der folgt im nächsten Blogartikel, sondern darum, welche funktionalen Bausteine eine solche Anwendung überhaupt benötigt. Unabhängig von der konkreten Gleichung oder technischen Domäne folgt diese Übersetzung in Software meist einem ähnlichen Muster.
Im Kern steht eine Funktion, die den Wärmestrom in Abhängigkeit von fünf Größen berechnet: den Temperaturen \(T_1\) und \(T_2\), der Wärmeleitfähigkeit \(\lambda\), der Wanddicke \(d\) und der Fläche \(A\). Während die Größen Teil des Domänenmodells sind lässt sich die Berechnungslogik zunächst als fachliches, konzeptionelles Service-Modul auffassen, unabhängig von Technologie oder Framework.
Damit dieses Modul genutzt werden kann, braucht es Eingabedaten. Dafür gibt es mehrere Wege:
- Über eine Benutzeroberfläche (Frontend): komfortable und intuitiv, ideal für interaktive Nutzung.
- Über eine textbasierte Schnittstelle (API, z.B. JSON): flexibel und automatisierbar, etwa für Skripte oder andere Anwendungen.
- Über eine Datenbankanbindung: anstelle direkter Eingaben können Materialien gewählt werden, deren Wärmeleitwerte automatisch aus einer hinterlegten Datenbank gezogen werden.
Ebenso wichtig wie die Eingabe ist die Ausgabe der Ergebnisse, entweder als Visualisierung in der Oberfläche oder als strukturierte API-Antwort. Hier eröffnen sich viele Möglichkeiten: von einfachen Zahlenwerten bis hin zu interaktiven Diagrammen oder Wandmodellen.
Damit sind im Wesentlichen die wichtigsten Software-Komponenten einer modernen Web-Applikation benannt. Was dabei schnell deutlich wird: Um eine scheinbar einfache Gleichung als Web-App verfügbar zu machen, braucht es eine ganze Menge an Infrastruktur: Logik, Schnittstellen, Datenhaltung und Darstellung. Und gleichzeitig gibt es kein einfaches 1:1 Mapping vom technisch-physikalischen Aufgabenstellung zur Softwarelösung.
Konzept der funktionalen Bausteine
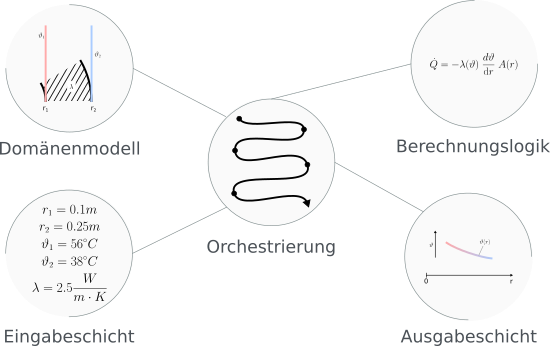
Um den Weg von der physikalischen Aufgabenstellung zur Software-Applikation auch für Ingenieure nachvollziehbar zu machen, ist eine zusätzliche Abstraktionsebene hilfreich: die funktionalen Bausteine.
Dieses Konzept liegt bewusst oberhalb von Physik und Software-Stack, ist aber domänenspezifisch, etwa für technische Berechnungssoftware, Ingenieurtools oder wissenschaftliche Anwendungen. Technische Applikationslogik lässt sich wie folgt abbilden:
- Domänenmodell - Welche fachlichen Objekte und Größen existieren?
- Berechnungslogik - Wie werden diese Größen miteinander verknüpft?
- Eingabeschicht - Wie gelangen konkrete Werte ins System?
- Ausgabeschicht - Wie werden Ergebnisse dargestellt oder weitergegeben?
- Orchestrierung - Wie greifen alle Bausteine kontrolliert ineinander?
Unabhängig von der konkreten Physik lassen sich viele technische Berechnungen in diese 5 funktionale Bausteine zerlegen, diese beschreiben keine konkrete Softwarearchitektur, sondern sind vielmehr eine funktionale Denkstruktur, die das Überführen von Ingenieurwissen in ein Softwareprodukt standardisiert. Dabei kommt der Orchestrierung eine besondere Rolle zu, sie enthält selbst keine fachliche Physik, sondern steuert den Ablauf. Sie nimmt Eingaben entgegen, ruft Berechnungen auf, kombiniert Ergebnisse und übergibt sie an die Ausgabeschicht.
Je nach Anwendung können diese Bausteine unterschiedlich ausgeprägt oder zusammengefasst sein und die Inhalte ändern sich, aber das Grundprinzip und die grundlegende Struktur bleiben gleich. Dabei geht es nicht um den Softwarestack, die Software-Architektur oder Schichten-Modell im Backend. Das Modell dient vielmehr als eine Art Übersetzer von Ingenieurwissen in strukturierte, wartbare Softwareanwendungen.
Der nächste Schritt ist dann die Überführung der funktionalen Bausteine in eine technische Softwarearchitektur und die konkrete Umsetzung in einem Software-Stack. Genau deshalb ist eine klare Struktur und ein durchdachtes Vorgehen entscheidend. Mein Ansatz folgt dem im ersten Teil vorgestellten 4-Phasen-Modell: Schnelligkeit → Persistenz → Flexibilität → Benutzerfreundlichkeit. Diese Phasen helfen, die Komplexität Schritt für Schritt zu beherrschen und die App mit den Anforderungen wachsen zu lassen.
Ausblick auf Teil 3
In diesem zweiten Teil meiner Einführungspost-Reihe lag der Fokus auf der technisch-physikalischen Grundlage: der eigentlichen Rechenlogik, die das Fundament jeder Berechnungsapplikation bildet und ihrer Abstrahierung in funktionale Bausteine. Gerade bei solchen Tools ist anfangs oft noch unklar, welche Funktionen später hinzukommen sollen. Daher ist es wichtig, von Beginn an Flexibilität und Erweiterbarkeit mitzudenken.
Genau dies möchte ich in Teil 3 meines Einführungspost aufgreifen und die Software-Architektur und den konkret gewählten Stack vorstellen: Wie die App technisch aufgebaut ist, welche Technologien ich einsetze und wie sich das 4-Phasen-Modell in der Praxis abbildet.
Wenn du Anregungen, Rückfragen oder Feedback hast, freue ich mich über den Austausch: .
Der Blog steht noch ganz am Anfang und wird in den kommenden Wochen und Monaten wachsen. Wenn du meine weitere Entwicklung verfolgen möchtest, schau gerne regelmäßig vorbei oder folge mir auf LinkedIn.